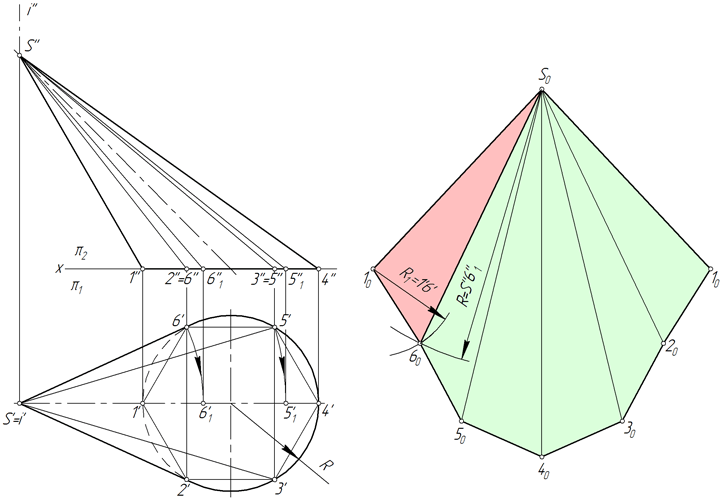
Фигура технического анализа треугольник: нисходящий, восходящий, симметричный

Числовой символизм валькнута

Числа играют очень важную роль во всех языческих религиях. Числовой символизм, соответственно, присущ и скандинавскому язычеству.

Числа, отраженные в изображении «узла павших» — это 3 и 9. Они имеют свое собственные сакральное значение. 9 – это число миров в скандинавской мифологии:

1. Мир богов или Асгард.
2. Мир людей или Мидгард.
3. Мир умерших или Хельхейм.
4. Мир ванов или Ванахейм.
5. Мир великанов или Йотунхейм.
6. Мир светлых альвов или Альвхейм.
7. Мир огненных великанов или Муспельхейм.
8. Мир ледяных великанов или Нифльхейм.
9. Мир карликов или Свартальфахейм.

Также 9 – число ветвей мирового ясеня Иггдрассиля (по одному
на каждый мир). 9 ветвей – основа рун старшего алфавита (футарка). 3 – число
норн (богинь судьбы), отражающее настоящее, прошлое и будущее.

Элементы остроугольного треугольника:

Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.

Рис. 4. Остроугольный треугольник и внешний угол

∠ ВСD – внешний угол

Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника

MС – медиана остроугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 6. Остроугольный треугольник и высота остроугольного треугольника

MС – высота остроугольного треугольника

Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.

Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника

MС – биссектриса угла остроугольного треугольника

Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства.

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства.

Значение валькнута в качестве татуировки

Татуировку в виде валькнута можно встретить и сейчас. Считается, что такой нательный рисунок указывает своему носителю верный путь.

Это подходит весьма амбициозным личностям, которые готовы жертвовать всем ради познания истины.

Такая татуировка показана людям, очень сильным духом, которые не привыкли сворачивать с выбранного пути.

Кстати, не рекомендуется применять в нательном рисунке валькнут в сочетании с рунами.

Считается, что так он приобретает совершенно ритуальный смысл (примерно как у воинов, идущих «на встречу с Одином»).

Символ «валькнут» имеет общее значение единения миров. Такой талисман помогает проникнуть в тайны мироздания, но одновременно и провоцирует проблемы в жизни носителя.

Преодоление этих невзгод означает, что человек готов к постижению тайных знаний.

Носитель валькнута должен быть очень силен духом и готов к противостоянию жизненным трудностям.

Предыдущая
СкандинавскиеМолот Тора (Мьельнир) — Значение амулета
Следующая
СкандинавскиеСкандинавский оберег шлем ужаса — агисхьяльм

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы

Стороны конструкции имеют следующее соотношение друг к другу:

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример

Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол

Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках

Понятие треугольника

Вспомним следующую аксиому для такого основного понятия геометрии, как прямая.

Аксиома 1: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.

Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда

Определение 1

Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.

Определение 2

Точки в рамках определения 1 называются вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 называются сторонами треугольника.

Треугольник будем обозначать тремя точками его вершин (рис. 1)

Восходящий и нисходящий клин

Восходящие и нисходящие клинья подобны восходящим и нисходящим треугольникам. Однако у них нет плоской стороны. Обе стороны клиньев имеют наклон в одном направлении.

Восходящий клин – это шаблон треугольника, где обе стороны наклонены вверх. Цена создает более высокие вершины и даже более высокие основания. Восходящий клин имеет сильный медвежий характер.

Когда вы замечаете пробой через нижний уровень восходящего клина, вы должны ожидать резкого падения цены, равного размеру паттерна. Поэтому пробои через нижний уровень клина используются для открытия коротких позиций.

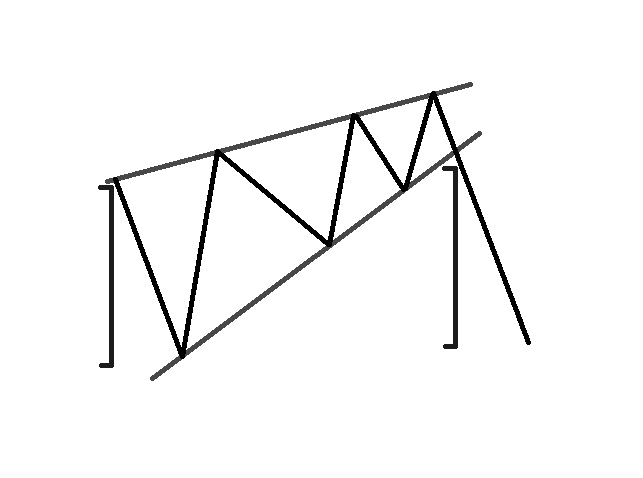
Обе стороны нисходящего клина наклонены вниз. Цена создает более низкие основания и более низкие вершины. Таким образом, две стороны треугольника сжимаются в одну точку. В противоположность восходящему клину, нисходящий клин имеет бычий характер. Следовательно, триггером для входа в сделку является верхняя линия. Когда цена преодолевает верхний уровень падающего клина, мы можем открывать бычьи позиции.

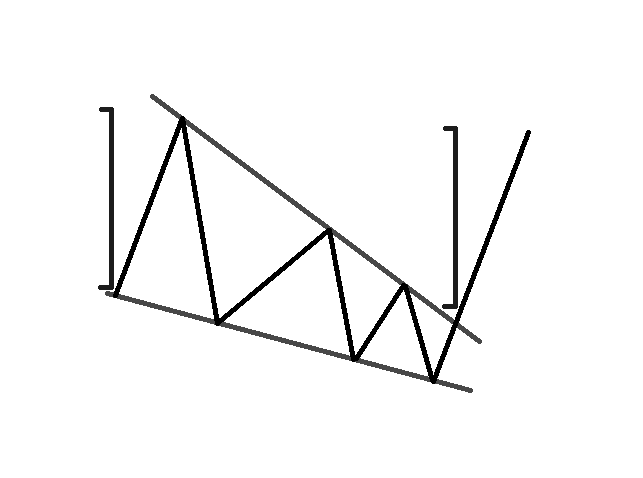
Клинья могут иметь продолжать текущий тренд или иметь разворотный характер. Когда после продолжительного движения цены появляется клин, мы ожидаем разворота тренда, когда клин появляется раньше в тренде, мы ожидаем, что это будет временная коррекция, которое продолжит основной тренд.

Как правило, более мощное формирование клина – это формирование потенциального разворота тренда, которое происходит после продолжительного движения на рынке.

Свойства равностороннего треугольника:

1. В равностороннем треугольнике все стороны равны между собой.

2. В равностороннем треугольнике углы равны и составляют 60°.

3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.

В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.

В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.

Рис. 2. Равносторонний треугольник

АK = BF = CD

4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.

Рис. 3. Равносторонний треугольник

R – радиус описанной окружности, r – радиус вписанной окружности

5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.

6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.

Рис. 4. Равносторонний треугольник

AO : OK = BO : OА = CO : OD = 2 : 1

Созвездие Треугольника

Точное происхождение названия этого созвездия неизвестно. Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.

Созвездие Треугольника. Иллюстрация из астрономического атласа «Уранография» Я. Гевелия

Второй признак равенства треугольников

Теорема:

Два треугольника равны, если у них равна одна из сторон и два прилежащих к ней угла.

Доказательство:

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых:

 AC = A₁C₁,  ∠A = ∠A₁  и  ∠C = ∠C₁.

Требуется доказать, что

ABC = A₁B₁C₁.

Если наложить  A₁B₁C₁  на  ABC  так, чтобы точка  A₁  совместилась с точкой  A  и сторона  A₁C₁  совместилась со стороной  AC,  то точка  C₁  совпадёт с точкой  C,  так как  A₁C₁ = AC.  Сторона  A₁B₁  совпадёт со стороной  AB,  так как  ∠A = ∠A₁.  Сторона  C₁B₁  совпадёт со стороной  CB, так как  ∠C = ∠C₁.  Вершина  B₁  совпадёт с вершиной  B,  так как  B  и  B₁  будут служить точками пересечения одних и тех же отрезков. Таким образом, треугольники совместятся. Теорема доказана.

Содержимое образований

Нервы и сосуды шеи

В каждом условном топографическом районе проходят кровеносные сосуды и нервные стволы, а также находятся органы. Знание содержимого имеет практическое клиническое значение, в частности для диагностики патологических процессов и выполнения хирургических вмешательств. Содержание треугольников передней области включает:

• Подчелюстной, включая район Пирогова – одноименная слюнная железа, регионарные лимфатические сосуды, лицевая артерии, подъязычный и язычный нервы.
• Сонный – основной нервно-сосудистый пучок, который может состоять из сонной артерии, яремной вены, блуждающего нерва.
• Лопаточно-трахеальный – позвоночная и общая сонная артерии и вены, нижнещитовидные кровеносные сосуды, блуждающий нерв и его ветви.

Наружные треугольники:

• Лопаточно-ключичный – подключичные артерия и вена, стволы плечевого нервного сплетения, грудной лимфатический проток.
• Лопаточно-трапециевидный – шейное нервное сплетение с ветвями, которые распространяются в кожу.

Во время выполнения любых инвазивных манипуляций топографическая анатомия треугольников, а также их содержимое, схемы расположения структур по отношению друг к другу обязательно учитываются для профилактики осложнений с необратимыми изменениями. Это касается крупных кровеносных сосудов, а также нервных стволов, повреждение которых недопустимо.

Топическая диагностика заболеваний структур шеи связана с визуализацией тканей. Она проводится при помощи методик, к которым относятся рентгенография, компьютерная, магнитно-резонансная томография, ультразвуковое исследование.

Названия геометрических фигур в картинках (23 ФОТО)

Геометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.

Объёмные геометрические фигуры

Разноцветные фигуры

Названия объёмных фигур на английском

Синие фигуры с английскими названиями

Синие фигуры с русскими названиями

Разноцветные фигуры с английскими названиями

Простые фигуры кубической сингонии

Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр

Весёлые геометрические фигуры

Shapes

Конус

Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник

Ромб

Призмы

Пирамиды

Свойства остроугольного треугольника:

Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 8. Остроугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 9. Остроугольный треугольник с равными боковыми сторонами

АВ = ВС

3. Сумма углов остроугольного треугольника равна 180°.

4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
1 792

Троица и треугольник

Начиная с ранних христиан треугольник был символом Святой Троицы. Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.

Схема Святой Троицы по католической традиции

Треугольники как символ Троицы в готической архитектуре

Как звучит?

Треугольник – это такой музыкальный инструмент, который не обладает конкретной высотой звучания. Ноты для него обычно создаются самыми разными по длительности и без ключей.

Однако тембр этого инструмента необыкновенен. Звучание его звонкое, яркое, чистое и как будто бы искрящееся. В оркестрах именно он в наибольшей мере влияет на уровень динамики и создаёт в музыкальном произведении определённый характер.

Звучание треугольника напрямую зависит от того, насколько сильным будет удар по нему. Так, нежный звук получается при практически невесомом ударе. При более резком звук выходит буквально режущим, блестящим и очень красочным.

Точка пересечения биссектрис треугольника

Теорема 2

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

Рассмотрим треугольник $ABC$, где $AM,\ BP,\ CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM\ и\ BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 3

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ,\ OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Теорема доказана.

Точка пересечения высот треугольника

Теорема 6

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что ${CC}_1\bot A_2B_2,\ {BB}_1\bot A_2C_2,\ {AA}_1\bot C_2B_2$. Следовательно, ${AA}_1,\ {BB}_1,\ {CC}_1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты ${AA}_1,\ {BB}_1,\ {CC}_1$ пересекаются в одной точке.

Теорема доказана.

Виды треугольников

Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.

Существует три вида треугольников по углам:

• остроугольные;
• прямоугольные;
• тупоугольные.

Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90.

Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.

Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.

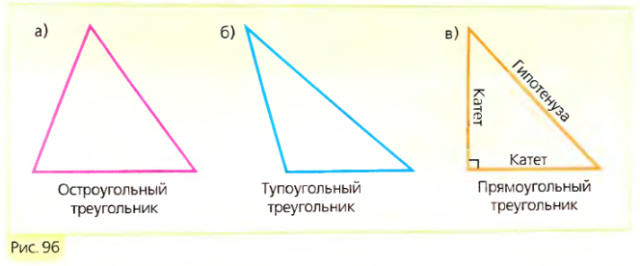
Рис. 2. Виды треугольников по углам.

Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.

Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.

Виды треугольников по сторонам:

• равносторонние;
• равнобедренные;
• разносторонние.

Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 60, то есть он всегда является остроугольным.

Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.

Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.

Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.

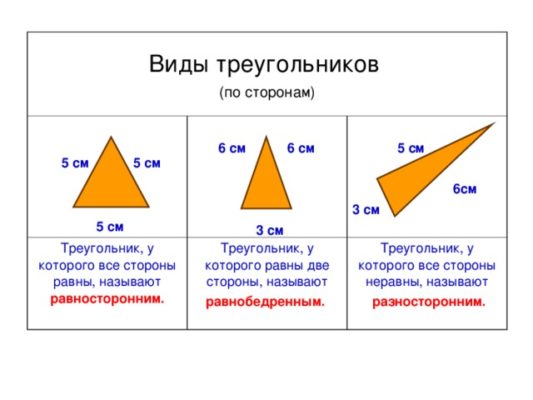
Рис. 3. Виды треугольников по сторонам.

Сумма всех углов треугольника, независимо от его вида, равна 1800.

Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.

Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основе и равны определенному числу. В такой фигуре углы пропорциональны соотношению 2:2:1.

Описание треугольников

Начиная писать любую статью, хочется сделать ее, прежде всего уникальной и неповторимой. Подписчики моего сайта, должны находить ответы на все свои вопросы в моих статьях. По этой причине, приходится перечитывать кучу литературы и статей с аналогичных моему сайтов.

В итоге оказывается, создать уникальную статью совсем не сложно. К сожалению, практически все владельцы форекс сайтов, скачивают информацию друг у друга, и практически все статьи как под копирку. Конечно это возмущает, не уж то нет своей головы, но да ладно, вернемся к теме.

Практически во всех книгах, и на всех сайтах, трейдеры сходятся во мнении, что фигура графического анализа треугольник — фигура неопределенности. И хотя ее классифицируют, как фигуру продолжения тренда, не всегда это срабатывает.

Виды треугольников

Всего имеется 4 вида треугольников, одна из них разворотная фигура, и три фигуры продолжения тренда. Надо понимать, что все это условно и к каждой сделке, нужно подходить индивидуально.

К разворотным фигурам, относится:

расходящийся треугольник.

К фигурам продолжения, относятся:

• симметричный треугольник;
• нисходящий треугольник;
• восходящий треугольник.

Построение треугольника

Построить любой из выше перечисленных треугольников, можно всего лишь по 4 точками.

По такому же принципу, строятся и остальные виды треугольников. В случае симметричного, нисходящего и восходящего треугольников, обязательное правило, линии должны сходились, для расширяющегося треугольника, расходились.

Пробой треугольника

В различных книгах по техническому анализу пишут: «Выход из треугольника, в большинстве случаев будет противоположный от входа». Это значит, если до начала формирования треугольника, тренд был вверх, то и выход из треугольника будет вверх (исключение, расходящийся треугольник). Но, в тех же книгах по трейдингу, встречаются фразы по типу: «Нельзя заранее определить в какую сторону будет выход». 

Поэтому предлагаю не гадать, а использовать единственно верный метод, дождаться выхода (пробоя) и следовать за ценой.

Если мы видим, что цену зажимают в фигуру технического анализа Треугольник, то чего нам торопиться? Цена никуда не убежит, есть время подождать. А вот когда произойдет пробой треугольника, это наш сигнал в какую сторону собирается двигаться рынок. Здесь то и можно вступать в игру. Входим на ретесте пробитого уровня, и торгуем по тренуд.

Где ставить take profit? 

Не решенным остался только один вопрос, где ставить take profit? 

Для расчета профита, нужно отложить максимальную ширину треугольника, от места пробой. Заложитесь на несколько пунктов в меньшую сторону и ждать тейка.

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и &angle;A=&angle;A₁. Докажем, что .

Так как &angle;A=&angle;A₁, то треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины A и A₁ совпадали, а стороны AB и AС наложились на лучи A₁B₁ и A₁C₁, соответственно.

Так как по условию теоремы AB=A₁B₁, AС=A₁С₁, то сторона AB совместится со стороной A₁B₁, а сторона AС − со стороной A₁С₁.Тогда совместятся B и B₁, C и С₁. Следовательно сторона BC совместится со стороной B₁C₁. То есть треугольники ABC и A₁B₁C₁ полностью совместятся. Теорема доказана.

Фигура треугольник в трейдинге

Теперь, когда мы обсудили большинство важных моделей треугольников, посмотрим, как их можно использовать в своей торговле.

На графике показаны пять примеров треугольников и их потенциальные результаты.

График начинается с большого симметричного треугольника. Цена создает три убывающие вершины и три увеличивающиеся основания на графике. Стрелка в начале треугольника измеряет его размер. Как видите, такая же стрелка применяется, когда цена преодолевает верхний уровень треугольника и указывает на потенциальную цель модели, которая фиксируется через неделю.

Между тем, на пути к повышению цены создается график восходящего клина. Как мы уже говорили, восходящий клин имеет медвежий потенциал. При пробое нижнего уровня клина мы замечаем небольшую коррекцию.

В конце бычьей тенденции цена создает еще один симметричный треугольник. Позже цена пробивает нижний уровень и завершает размер фигуры.

При снижении цены возникает медвежий вымпел. Это консолидация после первого импульса медвежьего тренда. Далее цена пробивает нижний уровень вымпела. На пути вниз мы видим, что цена завершает первую цель, которая равна размеру вымпела.

Затем цена создает модель разворота с двойным дном и переключается на бычье направление. На пути вверх ценовое действие возникает расширяющийся треугольник

Обратите внимание, что верхний и нижний уровни шаблона увеличиваются. В этом случае ожидаемое движение цены является медвежьим и должно быть равным размеру паттерна

Христианские варианты треугольника

В религиозной символике Средневековья появлялось много разновидностей подобных фигур:

1. Треугольник в сочетании с крестом символизировал смерть на кресте Иисуса за грехи человеческие, воскресение его Богом-Отцом, покаяние христиан и снисхождение Святого Духа.
2. Три рыбы, составляющие треугольник, означали: Иисус Христос, Сын Божий, Спаситель. Также они знаменовали Троицу.
3. Треугольник, содержащий греческие буквы Omicron, Omega и Nu. Эти буквы означают собой слова εγω ειμι ο ων, сказанные Богом Моисею из горящего куста (Исход 3:14), которые переводятся как «Я есть Сущий». Дословно фраза была взята из Септуагинты, древнегреческого перевода Ветхого Завета.
4. Три фигурки бегущих кроликов создают два треугольника, внутренний и внешний. Символ часто присутствовал как рельефный элемент архитектуры и деревянных деталей. Знак также знаменует Триединого Бога. Такое изображение встречается в настенной живописи древнего Египта и, возможно, тогда символизировало мужчину, женщину, потомство.

30+ лучших эскизов с описанием

Тату треугольник – необычный и красивый рисунок. Этот символ используется во многих культурах и религиях, откуда и был взят в качестве эскиза для уникальных татуировок

Просто так наносить этот рисунок на свое тело все-таки не стоит – важно понимать, какой именно смысл скрыт в выбранном эскизе. Если вас заинтересовала тату треугольник значение этого изображения подробно описывается в данной статье

Ознакомившись с материалом, вы поймете – действительно ли хотите видеть этот символ на своем теле.

Тату треугольник значение в разных культурах и религиях

Прежде, чем набить на свое тело татуировку с изображением треугольника, ознакомьтесь со значением рисунка в различных религиях и культурах.

1. Знаменитый древнегреческий философ Платон, ученик Сократа, утверждал, что треугольник – это символ «триединства» мира. Он ознаменует собой Землю, Небеса и Человека. В древнегреческой философии есть еще одно пояснение – это семья, а каждая вершина фигуры это член семьи — мать, отца и дитя.
2. По мнению буддистов в этом символе скрыт огонь.
3. Христиане уверены, что символ указывает на Святую Троицу.
4. Египтяне утверждают, что треугольник — это Триада.

Если говорить о том, что означает треугольник тату, то пояснений будет довольно много. Они зависят от того, какие дополнительные элементы имеет такое изображение и на чьем теле оно нанесено (мужчины или женщины).

Что означает треугольник тату: разные варианты и их значения

Если татуировка в виде треугольника нанесена на женское тело, то она будет указывать на три этапа жизни:

• юность;
• зрелость;
• старость.

В свою очередь мужчины вкладывают в треугольник совершенно другой смысл. В понимании представителей сильного пола, такая татуировка означает:

• физическую силу и духовность;
• мудрость и разум;
• красоту тела.

Филосовски настроенные люди утверждают, что в символе гармонично объединены разум, тело и бессмертие души. Довольно часто такую татуировку выбирают те, кто хочет подчеркнуть – он является гармонично развитой личностью.

Эскизов тату треугольник – неисчислимое количество. Например, встречаются картинки, на которых вершина слишком уж вытянута вверх. На других рисунках – она приплюснута. Наиболее распространенный вариант – равнобедренный треугольник. Хотя стоит признать, что четкой трактовки таких треугольников нет, а потому их накалывают не так уж и часто.

Относительно распространенный вариант – треугольник, повернутый вершиной вниз. Такую тату выбирают представительницы слабой половины человечества, что обусловлено определенным сексуальным подтекстом рисунка – этот треугольник напоминает место внизу женского животика.

Среди прочих вариантов тату треугольник можно отметить:

• треугольник, помещенный внутрь квадрата – показывает сочетание материального и духовного;
• три треугольника – символ здоровья и духовности, крепкой физической силы и прочности духа;
• цветной треугольник – личный оберег человека, владелец сам придумывает, какие цвета и оттенки использовать в оформлении.

Тату треугольник набивают на спину, на кисти, на плече, на предплечье, на лодыжку, но встречается и на других частях тела.

Посмотри видео ( 3 минуты 57 секунд )

tattoo-sketches.com

Бычий и медвежий вымпел

Вымпелы на графике имеют форму, аналогичную форме симметричных треугольников. Они обычно появляются во время трендов и имеют характер продолжения тренда.

Бычий вымпел похож на симметричный треугольник по внешнему виду, но его происходит после повышения цены. Поскольку вымпелы имеют характер продолжения тренда, бычий вымпел, скорее всего, продолжит текущий бычий тренд на графике. Когда верхняя сторона вымпела пробивается вверх, мы, вероятно, увидим движение цены, равное, по крайней мере, размеру вымпела.

При торговле вымпелами можно использовать вторую цель фиксации прибыли, чтобы получить большую прибыль. При расчете второй цели вы должны проанализировать движение цены. Вы можете установить цель 1:1 предыдущего этапа или 0,618. Когда тренд кажется сильным и имеет крутой уклон, движение 1: 1 будет подходящей второй целью, и во всех других случаях можно использовать 0,618.

Медвежий вымпел является зеркальным отражением бычьего вымпела. Медвежьи вымпелы начинаются со снижения цены и заканчиваются симметричным появлением треугольника. Поскольку вымпелы имеют тенденцию продолжения тренда, медвежьи вымпелы продолжат медвежий тренд.

Когда цена проходит через нижний уровень медвежьего вымпела, вы должны сначала попытаться захватить первую цель, которая равна размеру самого вымпела. Когда цена достигает этой цели, вы можете попытаться поймать дальнейшее снижение, которое равно размеру предыдущего этапа или 0,618.

Свойства тупоугольного треугольника:

Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 9. Тупоугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 10. Тупоугольный треугольник с равными боковыми сторонами

АВ = АС

3. Сумма углов тупоугольного треугольника равна 180°.

4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
4 223

Оккультизм XIX века

В середине позапрошлого столетия интерес к philosophia occulta получил широкое распространение по всей Европе и многим областям Северной Америки, став довольно модным явлением в средних и высших кругах общества.

С развитием наук и технологий появились разработки, подводящие идеи эзотеризма под научную основу. Было написано множество теоретических трудов, издано немало книг и журналов по различным направлениям оккультизма.

Поскольку в эзотерической традиции одним из главных принципов считается подчинение всех сущностей закону триединства, символ триады в «тайных учениях» наделен особой, мистической значимостью. В оккультных изданиях XIX века подобные изображения трактуются с точки зрения их глубокого смысла в эзотерике, а также сакральной роли западных и восточных религиозных систем.

Что из себя представляет фигура треугольник?

Фигура треугольник – это паттерн, сформированный на ценовом графике. Обычно он идентифицируется, когда вершины и основания цены движутся навстречу друг другу, как стороны треугольника. Когда верхний и нижний уровни треугольника взаимодействуют с ценой, трейдеры ожидают возможного пробоя. Таким образом, многие трейдеры, торгующие на пробой, используют формации треугольника для поиска точек входа.

На графиках можно увидеть различные типы треугольников. Можно выделить:

• Восходящий и нисходящий треугольник.
• Восходящий и нисходящий клин.
• Симметричный треугольник.
• Бычий и медвежий клин.
• Расширяющийся треугольник.

Прежде чем перейти к торговле треугольником, вы должны понять разницу между существующими формациями. Далее мы подробнее рассмотрим различные типы треугольников и соответствующие им торговые настройки. Как только вы овладеете этими знаниями, вы сможете добавить торговую стратегию фигуры треугольник в свой торговый арсенал.