Формулы вычисления площади произвольного четырёхугольника

[править] Формулы

Формулы в векторной и координатной форме

Введём обозначения:

\bar r_1=(x_1,y_1,z_1) — радиус-вектор первой точки;

\bar r_2=(x_2,y_2,z_2) — радиус-вектор второй точки;

\bar r_3=(x_3,y_3,z_3) — радиус-вектор третьей точки;

\bar r_4=(x_4,y_4,z_4) — радиус-вектор четвёртой точки;

\bar n=(A,B,C) — нормаль к плоскости, проходящей через три заданные точки;

S_Δ — площадь треугольника, построенного по трём заданным точкам;

S_четыр — площадь четырёхугольника, построенного по четырём заданным точкам.

где

Формула Брахмагупты

Рассмотрим четырёхугольники, вокруг которых можно описать окружность и у которых порядок следования вершин 1, 2, 3, 4. Для нахождения их площади можно использовать формулу Брахмагупты.

Введём обозначения:

a — длина стороны четырёхугольника, расположенной между первой и второй точками;

b — длина стороны четырёхугольника, расположенной между второй и третьей точками;

c — длина стороны четырёхугольника, расположенной между третьей и четвёртой точками;

d — длина стороны четырёхугольника, расположенной между первой и четвёртой точками;

p — полупериметр четырёхугольника, построенного по четырём заданным точкам.

где

• Когда одна из сторон четырёхугольника стремится к нулю, тогда формула Брахмагупты превращается в формулу Герона для площади треугольника.
• Когда четырёхугольник является прямоугольником и a≠b, тогда формула Брахмагупты превращается в формулу площади прямоугольника, S_{прямоуг}=ab, где c=a, d=b, p=a+b.
• Когда четырёхугольник является равнобедренной трапецией и b=d, тогда формула Брахмагупты превращается в формулу площади трапеции, S_{равн.трап}=h(a+c)/2, где h2=(p-a)(p-c), p-b=(a+c)/2.

Один из методов определения площади четырехугольника состоит в разбиении фигуры на два треугольника с помощью диагонали и в вычислении суммы площадей образовавшихся треугольников.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S =	1
   2

2. Какие формулы используют, чтобы рассчитать свайный фундамент и онлайн-сервисы для вычисления

   Формула площади треугольника по трем сторонам

   S = √()()()

3. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

   S =	1
   2

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

   S =
   4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   S =  ·

   где S — площадь треугольника, — длины сторон треугольника, — высота треугольника, — угол между сторонами и , — радиус вписанной окружности,
   R — радиус описанной окружности,

   =	+  +	— полупериметр треугольника.
   2

Формулы площади параллелограмма

1. Расчет площади воздуховодов и фасонных изделий: примеры и формулы

   Формула площади параллелограмма по длине стороны и высотеПлощадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = 

2. Формула площади параллелограмма по двум сторонам и углу между нимиПлощадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = 

3. Формула площади параллелограмма по двум диагоналям и углу между нимиПлощадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

   S =	1	12
   2

   где S — Площадь параллелограмма, — длины сторон параллелограмма, — длина высоты параллелограмма,₁, ₂ — длины диагоналей параллелограмма, — угол между сторонами параллелограмма, — угол между диагоналями параллелограмма.

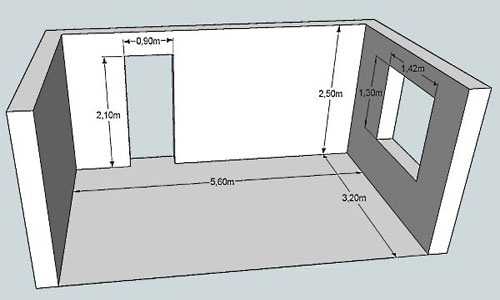
Как посчитать площадь стен

Чтобы определить площадь стен, нужно знать, как рассчитать периметр комнаты. Определение площади часто требуется для закупки всевозможных материалов для отделки. Кроме длины и ширины помещения, понадобится выяснить высоту комнаты, а также габариты проемов двери и окон.

При расчетах стоит учитывать, что высота потолков даже в одном помещении может варьироваться, особенно если комната мансардного типа. Отдельно вычисляются значения всех стен, а затем их них отнимаются оконные и дверные проемы.

Точные значения можно выявить с помощью калькулятора расчета площади стен комнаты. Иногда требуется определить объем помещения. В такой ситуации необходимо перемножить три значения: длину, ширину и высоту комнаты. Данный показатель меряется в кубических метрах.

Если помещение имеет разноуровневое зонирование, то можно провести такие расчеты:

• померить все участки стен. Замеры рекомендуется выполнять поближе к потолку;
• вычислить показатели площади по полу;
• на каждом вертикальном участке необходимо промерить длину и высоту, а затем данные значения перемножить;
• прибавьте показатели к значению пола.

У каждой комнаты есть оптимальные параметры, которые можно учитывать при планировке строительного объекта. Минимальный показатель жилого помещения равняется 8 кв. м. Комната общего назначения, такая как зал или гостиная может иметь площадь от 14 до 25 кв. м. Минимальный показатель высоты помещения составляет 240 см. Если потолок более трех метров, то такое пространство сложнее обогревать. Кухня должна иметь площадь не менее 6 кв. м.

Правильное вычисление площади помещения является гарантией качественного проведения ремонта. Такой подход позволит свести к минимуму затраты на приобретение материалов.

Ремонт – дело хлопотное, но приятное, ведь после него квартира или частный дом становятся более уютными, современными, располагающими к отдыху. «Как рассчитать площадь комнаты и стен?» – это, пожалуй, один из первых вопросов, которые возникают на горизонте переделок.

Можно не заниматься расчетами самостоятельно, а доверить это дело бригаде отделочников, которые и будут проводить ремонт. А что делать, если решение принято, и все работы будут выполняться своими руками? В этом случае расчет должен быть особо тщательный, так как отсутствие опыта может стать результатом нехватки или переизбытка того или иного материала.

Формулы площади выпуклого четырехугольника

1. Формула площади четырехугольника по длине диагоналей и углу между ними
   Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

   S =	1	1 2 sin
   2

   где S — площадь четырехугольника,₁, ₂ — длины диагоналей четырехугольника, — угол между диагоналями четырехугольника.

2. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
   Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружностиS =  · 

3. Формула площади четырехугольника по длине сторон и значению противоположных угловS = √()()()() —  cos2

   где S — площадь четырехугольника,, , , — длины сторон четырехугольника,

   =	+  +  +	— полупериметр четырехугольника,
   2

   =	+	— полусумма двух противоположных углов четырехугольника.
   2

4. Формула площади четырехугольника, вокруг которого можно описать окружностьS = √()()()()

Как посчитать квадратные метры комнаты

В каких случаях требуется квадратура помещения:

• При установке на кухню модуля из шкафов.
• При оплате коммунальных услуг, где сумма рассчитывается исходя из метража.
• При оплате рабочим после ремонта. Их тарифы также привязаны к площадям и количеству метров.
• При определении нормативов освещения вычисляется площадь.
• При установке отопления, вентиляции и кондиционирования требуется знать объем (кубатуру) помещения. Он вычисляется с помощью величины площади.
• При расчете количества закупаемых материалов для планируемого ремонта.

Чтобы правильно высчитать необходимые величины нужно знать несколько формул и уметь с их помощью рассчитать квадратные метры стен, потолка и пола.

Квадратура помещения нужна при оплате коммунальных услуг, определении нормативов освещения, установке отопления и покупке материалов для ремонта.

Для этого потребуются простейшие инструменты:

• Рулетка. Механическая, размером от 3 до 5 метров. Ею измерять лучше вдвоем, чтобы избежать погрешностей. Минимальная единица измерения – миллиметр. Электронная, измеряет лазерным лучом. Получить измерительную величину можно просто направив луч в начальную точку. Единица измерения здесь – миллиметр или сантиметр.

  Некоторые «умные» рулетки могут сразу высчитывать площадь помещения, не измеряя дополнительно что-то. С измерениями такой рулеткой можно справиться в одиночку, без дополнительной помощи. Плюс в быстроте измерений и расчетов. Минус в дороговизне и проблемах с измерением неправильных помещений.

• Калькулятор. Также для удобства в расчетах разработаны специальные компьютерные программы.
• Угольник строительный. Должен быть с длинными сторонами – в этом случае замеры получатся более точными.
• Блокнот или тетрадь для занесения всех схем, измерений, расчетов.
• Уровень. С его помощью можно рассчитать отклонения вертикали/горизонтали.

Прежде чем приступить к измерениям и расчетам, нужно подготовить все необходимые инструменты.

1. Первое, что нужно сделать – это узнать, как рассчитывается квадратный метр. Здесь пригодится рулетка со шкалой в сантиметрах и метрах.
2. Затем измеряется длина помещения и его ширина. Причем, ширина измеряется, прикладывая рулетку строго перпендикулярно длине.
3. Измерения записываются вплоть до сантиметра. В сторону метров округлять не стоит.

Для измерения размеров помещения нужна обычная рулетка. Но существуют и “умные рулетки”. Они могут сразу высчитывать общую площадь.

Чтобы рассчитать квадраты на калькуляторе, нужно измеренную величину записать следующим образом: 1м=0.01 см. Если предположить, что длина комнаты – 3 метра 56 см, то на калькуляторе набрать 3,56. То же самое касается и ширины. В итоге, умножить длину комнаты на ее же ширину и получить величину квадратуры измеряемого помещения.

Для расчетов вам понадобится калькулятор и знание формул.

Для того, чтобы корректно измерить помещение, желательно освободить хотя бы две ее стороны от мебели и лишних предметов. В этом случае идеально измерять комнату на стадии ремонта.

Рулетка должна хорошо прилегать к измеряемой поверхности. Длину требуется измерить вдоль стены (или стен, если форма измеряемой фигуры не правильная). В начале измерений лучше проверить прямоугольность, измерив рулеткой диагонали помещения и сравнив цифры. Таким образом уточняется правильность формы.

Можно воспользоваться лазерной рулеткой. Такие дальномеры стали незаменимыми помощниками специалистов и умеют запоминать измерения и вычислять по ним площадь или кубатуру помещения.

А вот чтобы проверить прямые линии понадобится уровень. Реже большой строительный угольник или самодельный циркуль.

Уровень – инструмент для оценки соответствия поверхностей вертикальной и горизонтальной плоскости относительно земли.

Расчеты можно сразу переносить на схему. Обязательно измерять помещение несколько раз, во избежание ошибок. Во время замеров быть внимательным и собранным, следить абсолютно за всеми мелочами, которые могут повлиять на величины.

Площадь комнаты можно вычислить с помощью простой школьной формулы:

S=A*B.

• S – площадь;
• A – длина;
• B – ширина.

Подобным же образом можно вычислить и площадь каждой стены, пола и потолка.
В случае если помещение треугольной формы – нужно измерить длину и ширину, умножить друг на друга и разделить на 2.

Или по формуле:

S = (А*В)/2.

Площадь комнаты можно вычислить с помощью простой школьной формулы.

Расчет площади стен

Для подсчета необходимо воспользоваться известной из школы формулой площади прямоугольника.

Даже если комната самой «неправильной» формы, стены можно «развернуть» (разумеется, мысленно), и мы получим прямоугольник с длиной, равной периметру комнаты, и высотой, равной высоте комнаты.

А площадь прямоугольника равна произведению его сторон. Одна из сторон – периметр комнаты, другая – ее высота. Периметр комнаты – это сумма длин всех сторон плоской фигуры, представляющей пол, или, проще говоря, длина всех плинтусов.

Прямоугольная комната

Если комната простой формы, длину периметра можно измерить, сделав несколько необходимых измерений. Высота же измеряется обычно по любому углу комнаты, от пола до потолка. Линейные размеры следует измерять в метрах, тогда площадь выразится в квадратных метрах.

Пример: Периметр комнаты 13,90 м, высота 2,65 м. Площадь стен = 13,90 х 2,65 = 36,84 кв. м.

Для расчета периметра прямоугольной комнаты достаточно измерить длину и ширину комнаты, сложить их и умножить на 2.

Пример: длина 4,1 м, ширина 2,85 м. Периметр = 2 х (4,1 + 2,85) = 13,90 (м).

Неправильная форма

Периметр комнаты неправильной формы можно измерить, тщательно протянув вдоль периметра по плинтусам бечевку или провод, при этом следует обогнуть бечевкой все выступы, изгибы, а затем измерить рулеткой длину участка бечевки, соответствующую периметру.

Форма стен может усложняться наличием ниш и выступающих частей. Иногда этими элементами можно пренебречь, при необходимости же их учета необходимо по формуле площади прямоугольника — учесть всю эту дополнительную площадь.

Смотрите в следующем видео — как рассчитать площадь стен:

В виде трапеции

У комнаты в виде трапеции из 4 стен две противолежащие параллельны друг другу, а две другие нет. В этом случае можно отдельно измерить длины всех 4 сторон и сложить. Это и будет периметр комнаты.

Существует сложная формула, позволяющая вычислить по измеренной длине 3 сторон четвертую, но проще измерить, чем вычислить.

Пример: Стороны комнаты с полом в виде трапеции 3, 4, 6 и 5 м. Периметр = 3 + 4 + 6 + 5 = 18 (м).

Округлой формы

Если комната строго круглой формы, периметр можно вычислить, измерив ее поперечник (диаметр) и умножив его на число «пи», равное (с округлением) 3,14.

Пример: поперечник 2,7 м, периметр = 3,14 x 2,7 = 8,48 (м).

Участки округлой формы придется посчитать отдельно, измерив бечевкой или гибкой рулеткой длину округлой части и прибавив ее к измеренным прямолинейным участкам периметра.

Формулы для нахождения площади

Через две стороны

Площадь прямоугольника через две стороны можно вычислить по формуле:

\(S=ab\)

где a, b — соседние стороны прямоугольника.

Через диагонали и синус угла между ними

Для того, чтобы найти площадь прямоугольника через диагонали и синус угла, нужно воспользоваться формулой:

\(S=\frac{d^2\sin\alpha}2\)

где \(d \) — диагональ, \(\alpha\) — угол между диагоналями (острый).

Через любую сторону и диагональ

Чтобы определить площадь прямоугольника через любую сторону и диагональ, нужно воспользоваться формулой:

\(S=a\sqrt{d^2-a^2}=b\sqrt{d^2-b^2}\)

где a, b — соседние стороны прямоугольника, d — диагональ.

Через сторону и диаметр описанной окружности

Чтобы узнать площадь прямоугольника через сторону и диаметр описанной окружности, нужно воспользоваться формулой:

\(S=a\sqrt{D^2-a^2}=b\sqrt{D^2-b^2}\)

где a, b — соседние стороны прямоугольника, D — диаметр описанной окружности.

Через сторону и радиус описанной окружности

Вычисление площади прямоугольника через сторону и радиус описанной окружности происходит по формуле:

\(S=a\sqrt{4R^2-a^2}=b\sqrt{4R^2-b^2}\)

где a, b — соседние стороны прямоугольника, R — радиус описанной окружности.

Через сторону и периметр

Чтобы посчитать площадь прямоугольника через сторону и периметр, нужно воспользоваться формулой:

\(S=\frac{Pa-2a^2}2=\frac{Pb-2b^2}2\)

где a, b — соседние стороны прямоугольника, Р — периметр.

Через радиус описанной окружности и синус угла между диагоналями

Способ нахождения площади прямоугольника через радиус окружности и синус угла между диагоналями происходит по формуле:

\(S=\frac{4R^2\sin\alpha}2\)

Посчитать площадь неправильного прямоугольника

Если Вам необходима помощь справочно-правового характера (у Вас сложный случай, и Вы не знаете как оформить документы, в МФЦ необоснованно требуют дополнительные бумаги и справки или вовсе отказывают), то мы предлагаем бесплатную юридическую консультацию:

• Для жителей Москвы и МО — +7 (499) 110-86-37
• Санкт-Петербург и Лен. область — +7 (812) 426-14-07 Доб. 366

Между тем, для решения множества практических задач нередко приходится иметь дело с неправильными геометрическими фигурами. С этой проблемой человек сталкивается и при определении размеров дачного участка или придомовой территории, и при расчете количества ткани для шитья, и еще во многих случаях. Рассмотрите геометрическую фигуру и определите, какие ее параметры вам известны. В зависимости от заданных параметров и выберите способ определения площади. Один из самых распространенных методов — провести диагонали из одного угла ко всем остальным вершинам.

Во многих случаях может потребоваться расчет площади земельного участка, например, в случае покупки, сдачи в аренду или проведении межевания.

Воспользовавшись онлайн калькулятором для вычисления площади прямоугольника, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал. В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Площадь неправильного 4-х угольника с заданными сторонами

Регистрация Вход. Ответы Mail. Вопросы — лидеры Где краткие содержания для читательского дневника? Помогите пожалуйста решить задание 1 ставка.

Как посчитать площадь неправильного прямоугольника с разными сторонами?

Во многих случаях может потребоваться расчет площади земельного участка, например, в случае покупки, сдачи в аренду или проведении межевания. Если надел имеет форму квадрата или правильного прямоугольника, то сделать это достаточно просто. Но как произвести расчет, если участок неправильной формы? В этом случае лучше всего воспользоваться онлайн-калькулятором. Для расчета площади участка четырехугольной формы выполните следующие действия:.

Дорогие читатели, информация в статье могла устареть, воспользуйтесь бесплатной консультацией позвонив по телефонам:. Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Основные способы

Существует три основных способа определения площадей:

• аналитический;
• графический;
• механический.

определение площади

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

При механическом способе площадь определяется по плану с помощью специального устройства — планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Наиболее точным является аналитический метод. На точность этого метода влияют только погрешности полевых измерений.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

S= 0,5*∑(Xi*(Yi+1-Yi-1), где:

• Xi и Yi — координаты i-той характерной точки участка, имеющего вид многоугольника;
• i — порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n — число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

Sт=0,5*(a+b)*h, где:

• a и b — основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

р=0,5(а+B+c+d), где:

a,b,c,d — величины сторон.

Тогда площадь участка Sу будет равна:

Sy=√(p-a)(p-b)(p-c)(p-d).

В некоторых случаях, когда имеется много точек поворота, аналитический расчет площади участка производится с использованием данных об углах азимута.

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

В некоторых случаях участки имеют криволинейную форму, которую трудно аппроксимировать простыми фигурами. В таких случаях могут использоваться палетки.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.

Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.

Механический способ

Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.

Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом. На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль. Точность метода зависит от размеров участка и свойств плана.

Формулы для площадей четырехугольников

Четырехугольник	Рисунок	Формула площади	Обозначения
		S = ab	a и b – смежные стороны
		d – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R	R – радиус ,φ – любой из четырёх углов между
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = absin φ	a и b – смежные стороны,φ – угол между ними
		d1, d2 – , φ – любой из четырёх углов между ними
		S = a2	a – сторона квадрата
	S = 4r2	r – радиус
		d – квадрата
	S = 2R2 Получается из верхней формулы подстановкой d = 2R	R – радиус
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ	a – сторона,φ – любой из четырёх углов ромба
		d1, d2 –
	S = 2ar	a – сторона,r – радиус
		r – радиус ,φ – любой из четырёх углов ромба
			a и b – основания,h –
	S = m h	m – ,h –
		d1, d2 – , φ – любой из четырёх углов между ними
		a и b – основания,c и d  – боковые стороны
		S = ab sin φ	a и b – неравные стороны,φ – угол между ними
		a и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r	a и b – неравные стороны,r – радиус
		d1, d2 –
Произвольный выпуклый четырёхугольник			d1, d2 – , φ – любой из четырёх углов между ними
		,	a, b, c, d – длины сторон четырёхугольника,p – , Формулу называют «Формула Брахмагупты»

	S = ab гдеa и b – смежные стороны
	гдеd – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = absin φ гдеa и b – смежные стороны,φ – угол между ними
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	S = a2 гдеa – сторона квадрата
	S = 4r2 гдеr – радиус
	гдеd – квадрата
	S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба
	гдеd1, d2 –
	S = 2ar гдеa – сторона,r – радиус
	гдеr – радиус ,φ – любой из четырёх углов ромба
	гдеa и b – основания,h –
	S = m h гдеm – ,h –
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	гдеa и b – основания,c и d  – боковые стороны
	S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними
	гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r гдеa и b – неравные стороны,r – радиус
	гдеd1, d2 –
Произвольный выпуклый четырёхугольник
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	, гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

S = ab гдеa и b – смежные стороны

гдеd – диагональ,φ – любой из четырёх углов между

S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = absin φ гдеa и b – смежные стороны,φ – угол между ними

гдеd1, d2 – , φ – любой из четырёх углов между ними

S = a2 гдеa – сторона квадрата

S = 4r2 гдеr – радиус

гдеd – квадрата

S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба

гдеd1, d2 –

S = 2ar гдеa – сторона,r – радиус

гдеr – радиус ,φ – любой из четырёх углов ромба

гдеa и b – основания,h –

S = m h гдеm – ,h –

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa и b – основания,c и d  – боковые стороны,

S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними

гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.

S = (a + b) r гдеa и b – неравные стороны,r – радиус

гдеd1, d2 –

Произвольный выпуклый четырёхугольник

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

Как посчитать площадь комнаты: методика расчета по полу

Можно рассчитать площадь пола. Данная процедура состоит из таких этапов. Прежде всего, необходимо освободить стены помещения. Лучше проводить измерения в пустом помещении. Если помещение прямоугольное, то можно перемножить две стороны

В реальности стороны могут немного отличаться, поэтому так важно мерить все стороны. В некоторых случаях комната может быть не правильной конфигурации

В такой ситуации все пространство делится на отдельные прямоугольники. При этом можно нарисовать схему со всеми размерами. Затем считается площадь отдельных участков. Кстати, помещение не обязательно будет состоять только из прямоугольников. Оно может содержать треугольники и даже круги.

В таблице можно посмотреть соответствие площади на полу с показателями для стен при определенной высоте потолка

Если вы не знаете, как посчитать квадратные метры комнаты, то можно воспользоваться специальным калькулятором. При вычислении габаритов не обязательно соблюдать все размеры до сантиметра. Часто применяется округление значений. Иногда  требуется учитывать разные углубления и выступы в стенах.

При расчетах важно учитывать и их предназначение. Если нужно узнать значения для монтажа теплого пола, то можно не учитывать пространство, занятое тяжелой мебелью

Есть варианты, когда в помещении используются разные уровни пола. В подобной ситуации также требуется поделить комнату на отдельные зоны. Не стоит осуществлять замеры по стене, так как она может иметь кривую поверхность.

Сложно определить площадь по полу, имеющего разнообразные выступы в виде волн или полукругов.

Полы сложной конфигурации требуют особой внимательности и использования специальных формул

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

S = ((a + b+ c + d)/2)*r

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Как найти площадь многоугольника

Все, что имеет больше двух углов, является многоугольником, в том числе и треугольник. Рассмотрим, как найти площадь многоугольников.

1

Как найти площадь многоугольника – треугольник

• S = 1/2×h×b, где h – высота, а b – сторона.
• S = 1/2 a×b×sinα, где а и b – стороны треугольника, а sinα – синус угла между ними.
• S = √p×(p-a)×(p-b)×(p-c), где p – половина периметра, а, b, c – стороны. Если известны все стороны треугольника, то найти площадь можно именно по этой формуле.
• S = r×p, где r – радиус вписанной окружности, а p – половина периметра. Если в треугольник вписана окружность, то для нахождения площади можно использовать эту формулу.
• S = abc/4R, где a, b, c – стороны треугольника, а R – радиус описанной окружности. Если треугольник вписан в окружность, для нахождения площади треугольника можно использовать эту формулу.

Прямоугольный треугольник

• S = 1/2×ab, где a и b – катеты прямоугольного треугольника.
• S = d×e, где d и e отрезки гипотенузы, образованные при касании вписанной окружности об гипотенузу.
• S = (p-a)×(p-b), где p – половина периметра, а и b – катеты.

Равнобедренный треугольник

• S = 1/2×a²×sina, где а – бедро треугольника, sina же – угол между бедрами.
• S = b²/4tgα/2, где b – основание треугольника, а tgα – угол между бедрами.

Равносторонний треугольник

• S = √3×a²/4, где а – сторона треугольника (любая, так как в равностороннем треугольнике все стороны равны).
• S = 3√3×R²/4, где R – радиус окружности, в которую вписан треугольник.
• S = 3√3×r², где r – радиус окружности, которая вписана в треугольник.
• S = h²/√3, где h – высота равностороннего треугольника.

2

Как найти площадь многоугольника – квадрат

• S = a², а – сторона квадрата. Так как все стороны квадрата равны, достаточно умножить одну его сторону на другую.
• S = d²/2, где d – диагональ квадрата.

3

Как найти площадь многоугольника – прямоугольник

• S = a×b, где a и b – стороны прямоугольника. Так как противолежащие стороны в прямоугольнике равны, достаточно умножить одну его сторону (длину) на не противолежащую, перпендикулярную сторону (ширину).
• S = a²+b²=c², где a – ширина, b – длина, а c – диагональ. Диагональ делит прямоугольник на два прямоугольных треугольника и если в условии задачи дана одна сторона прямоугольника и его диагональ, несложно будет найти и третью сторону, использую теорему Пифагора. После того как мы найдем эту сторону, ищем площадь по стандартной формуле a×b. Пример: Ширина прямоугольника – 3см, диагональ – 5 см. Найти площадь. Пишем 3² + x² = 5².  x² = 16 => x = 4. S = a×b = 3×4=12. Ответ: S прямоугольника = 12см²

4

Как найти площадь многоугольника – трапеция

• S = (a+b)×h/2, где a – маленькое, b – большое основание трапеции, h – высота.
• S = h×m, где h – высота, m – средняя линия трапеции, равная половине суммы оснований – 1/2×(a+b).
• S = 1/2×d1×d2×sinα, где d1 и d2 – диагонали трапеции, а sinα – синус угла между ними.
• S = a+b/2×√c²-((b-a)²+c²-d²/2(b-a))², где a и b – основания трапеции, c и d – остальные две стороны.

S = 4r²/sinα, где r – радиус вписанной окружности, а sinα – синус угла между стороной и основанием.

5

Площадь правильного многоугольника

• S = r×p = 1/2×r×n×a, где r – радиус вписанной окружности, p – половина периметра. Для того чтобы найти площадь любого правильного многоугольника, нужно разбить его на равные треугольники с общей вершиной в центре вписанной окружности.
• S = n×a²/4tg(360°/2n), где n – число сторон правильного многоугольника, а – длина стороны.Также вычислить площадь правильного многоугольника поможет данный онлайн сервис. Просто вставьте нужное значение и получите ответ.

6

Площадь неправильного многоугольника

Площадь неправильного многоугольника можно найти с помощью координат его вершин. Если в условии задачи даны вышеупомянутые координаты, то выполняем следующее:

• Составляем таблицу указывая букву, обозначающую вершину и соответствующие координаты (x; y).
• Умножаем значение x одной вершины на значение y второй и так далее.
• Складываем все значение, получаем какое-то число.

Составляем точно такую таблицу, по такому же принципу умножаем y координату одной вершины на x координату второй, складываем получившиеся значения.

От суммы значений первой таблицы отнимаем сумму значений второй таблицы.

Полученное число делим на 2 и тем самым находим площадь неправильного многоугольника.

Первая полоса

Беременность

Как не набрать лишний вес во время беременности